HAL Id: tel-00805547
https://tel.archives-ouvertes.fr/tel-00805547
Submitted on 28 Mar 2013
HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci- entific research documents, whether they are pub- lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Sylvie Icart
To cite this version:
Sylvie Icart. Matrices polynomiales et égalisation de canal. Traitement du signal et de l’image [eess.SP]. Université Nice Sophia Antipolis, 2013. �tel-00805547�
Sylvie Icart
Mémoire en vue de l’obtention d’une
Habilitation à Diriger des Recherches
Université de Nice-Sophia Antipolis Laboratoire I3S - CNRS
Polytech’Nice-Sophia Département Electronique ED STIC
1er mars 2013 Président : Jean-François Lafay
Rapporteurs : Vladimir Kučera MIAS Éric Moreau ISITV
Martine Olivi INRIA
Examinateurs : Pierre Comon GIPSA Lab Jean-François Lafay IRCCYN
L’Habilitation à Diriger des Recherches est un long chemin, merci à ceux qui m’ont accompagnée.
Merci à Vladimir Kučera, spécialiste des matrices polynomiales et ration- nelles de m’avoir fait l’honneur d’être rapporteur de cette thèse et d’être venu assister à la soutenance malgré ses nombreuses occupations.
Merci à Eric Moreau d’avoir accepté de rapporter sur mon travail après avoir accepté de rapporter sur les travaux des doctorants que j’ai encadrés.
Je souhaite que nous ayons encore l’occasion de travailler souvent ensemble.
Merci à Martine Olivi d’avoir accepté d’être rapporteur. Même si nous sommes proches géographiquement et thématiquement, nous n’avions jamais eu l’opportunité de travailler ensemble. J’espère que cette HDR ouvre la voie à une longue et fructueuse collaboration.
Je suis ravie d’avoir un automaticien, un traiteur du signal et une mathéma- ticienne comme rapporteurs, mon travail se situant à la frontière de ces trois disciplines.
Merci à Pierre Comon pour toutes ces années de collaboration et d’en- couragements. Il est parti vers d’autres horizons, mais les moyens techniques actuels vont nous permettre, à n’en pas douter, de poursuivre nos travaux.
Merci à Jean-François Lafay qui a présidé le jury de cette HDR et avec qui j’ai fait mes premiers pas en recherche. Il m’a donné son goût pour l’au- tomatique, les cours bien écrits et pour les démonstrations rigoureuses. Le temps a (trop) vite passé.
Merci à Viviane, Micheline et Marie-Pierre pour leur gentillesse, leur sou- rire et leur efficacité, ainsi qu’à toute l’équipe administrative et technique qui nous permet de travailler dans de bonnes conditions à l’I3S.
Merci à Gérard Favier qui a été le premier lecteur de ce manuscrit pour ses remarques pertinentes. Et merci à tous ceux de notre équipe-thème-projet avec qui je partage le thé venu des 5 continents.
La pause de midi est un moyen de refaire le monde, tout en courant plus ou moins vite avec l’équipe I3S-INRIA-assimilés. Merci en particulier à notre
"coach" Jean-Claude Bermond, grâce à ses conseils avisés j’ai pu faire moins de 4 heures au marathon et me décider à m’inscrire à l’HDR. Merci à Laure pour ses blagues de course et pour son amitié et à Philippe qui apprivoise les canards.
Merci à ma sœur et mes filles Laurane et Solène - mon or et mon soleil - qui m’ont soutenue à la fin de ce parcours, et à mon frère qui m’aide toujours à faire beaucoup de poussière.
avec qui j’ai beaucoup trouvé.
1 Introduction 5
2 Curriculum vitæ 7
2.1 Formation . . . 7
2.2 Expérience professionnelle . . . 7
2.3 Activités d’Enseignement . . . 8
2.4 Fonctions d’intérêt collectif . . . 11
2.5 Activités de Recherche . . . 13
3 Matrices L-polynomiales et égalisation 17 3.1 Polynômes de Laurent . . . 17
3.1.1 Notations . . . 18
3.1.2 Propriétés et définitions . . . 18
3.2 Matrices polynomiales de Laurent . . . 24
3.2.1 Forme de Smith des matrices polynomiales de Laurent 24 3.2.2 Ordre d’une matrice polynomiale de Laurent . . . 28
3.2.3 Para-conjugaison et forme hermitienne . . . 32
3.2.4 Matrice L-polynomiale para-hermitienne . . . 33
3.2.5 Matrice L-polynomiale para-unitaire . . . 39
3.3 Diagonalisation d’une matrice polynomiale . . . 45
3.3.1 Diagonalisation d’une matrice polynomiale normale . . 45
3.3.2 Valeurs singulières d’une fonction continue sur le cercle à valeurs dans Cn×n. . . 46
3.3.3 Diagonalisation d’une matrice AAH continue sur le cercle . . . 48
3.3.4 Presque-diagonalisation d’une matrice para-hermitienne 49 3.4 Matrices polynomiales et égalisation . . . 52
3.4.1 Problème de l’égalisation aveugle de canaux de com- munication . . . 52
3.4.2 Mélanges instantanés . . . 53
3.4.3 Mélanges convolutifs FIR . . . 53 1
3.4.4 Algorithmes de diagonalisation de L-matrices . . . 54
4 Conclusion et perspectives 57
5 Bibliographie 61
5.1 Publications . . . 61 5.2 Références . . . 64
A Quelques définitions classiques 69
B Publications choisies 73
R ensemble des nombres réels C ensemble des nombres complexes C∗ C\ {0}
C cercle unité
unité imaginaire 2 =−1 a scalaire (réel ou complexe)
v tableau à n lignes et une colonne (vecteur)
A matrice
0 matrice nulle I matrice identité
In matrice identité de taille n×n a∗ conjugué de a
aij élément de la ie ligne et je colonne de la matrice A AH matrice Atransposée conjuguée
A(z)e matrice para-conjuguée de A définie par A(z) =e AH(z1∗),∀z ∈C∗ C[z] anneau des polynômes en l’indéterminée z et à coefficients dans C C[z−1] anneau des polynômes en l’indéterminée z−1 et à coefficients dans C C[z, z−1] anneau des polynômes de Laurent en l’indéterminée z ie des poly- nômes ayant des puissances positives et négatives de z appelés aussi L-polynômes
U groupe des éléments inversibles de C[z, z−1] (monômes non nuls) Cn[z, z−1] ensemble des tableaux àn lignes et une colonne dont les éléments
sont des polynômes de Laurent 3
Cn×n[z, z−1] ensemble des matrices n ×n dont les éléments sont des poly- nômes de Laurent, ou encore matrices L-polynomiales
e
p(z) polynôme para-conjugué de p défini par p(z) =e p∗(z1∗),∀z ∈C∗
deg(p) degré en la variable z d’un polynôme p∈C[z] ou en la variable z−1 d’un polynôme p∈C[z−1]
d(p) L-degré d’un polynôme p ∈ C[z, z−1], soit degré en la variable z du polynôme associé à p(z)
N degré de MacMillan d’une matrice ∈Cn×n[z−1]
LS∼ équivalence au sens de Smith de deux matrices L-polynomiales C(z) corps des fractions rationnelles en l’indéterminée z et à coefficients
dans C
Cs(z) anneau des fractions rationnelles stables (pôles à l’intérieur du disque unité)
C(R) ensemble des fonctions continues définies sur le cercleC à valeurs dans R
C1(Cn) ensemble des fonctions continues f définies sur le cercle C à valeurs dans Cn tq f(Ω)f(Ω)H = 1,∀Ω∈ C
1C fonction tq 1C(Ω) = 1,∀Ω∈ C 0C fonction tq 0C(Ω) = 0,∀Ω∈ C
Introduction
Dans la théorie des systèmes linéaires multivariables, les matrices inter- viennent naturellement afin d’exprimer de manière synthétique les liens unis- sant les signaux d’entrée et de sortie. Dans le cadre des systèmes linéaires à temps continu invariants dans le temps, les transformées de Laplace des signaux d’entrée et de sortie sont reliées par une matrice de transfert dont chaque élément est une fraction rationnelle de la variable de Laplace : on ma- nipule alors des matrices rationnelles. Une fraction rationnelle est le quotient de deux polynômes, c’est également le cas pour les matrices rationnelles, mais les notions de numérateur et de dénominateur sont un peu plus délicates, no- tamment car le produit matriciel n’est pas commutatif et que la notion de primarité entre deux facteurs polynomiaux matriciels n’est pas aussi simple que dans le cas scalaire où elle se résume à l’absence de zéro commun [54].
Dans le cas des systèmes linéaires multivariables à temps discret, les trans- formées en z des signaux d’entrée et de sortie sont reliées par une matrice de transfert qui est une matrice rationnelle dans le cas des systèmes à ré- ponse impulsionnelle infinie et une matrice polynomiale en z−1 dans le cas des systèmes à réponse impulsionnelle finie.
Les propriétés de stabilité, causalité, observabilité, commandabilité, mini- malité des systèmes sont ainsi bien connues, les références en la matière étant les livres de Kailath [54] pour les systèmes à temps continu en automatique et Vaidyanathan [80] pour les systèmes à temps discret en traitement du signal. Les matrices polynomiales et rationnelles ont tout d’abord été utili- sées pour les problèmes d’automatique et de commande, voir par exemple les travaux de Kučera [55], Vidyasagar [81], ou le travail collectif [73], elles inter- viennent dorénavant aussi en télécommunication [77, 80, 53] notamment via les méthodes de type sous-espaces pour l’identification aveugle [64, 50, 61].
Dans ce mémoire, nous nous focaliserons sur un type de matrices par- ticulier : les matrices polynomiales de Laurent, dont les éléments sont des
5
polynômes de Laurent, c’est à dire des polynômes avec des puissances posi- tives et négatives de la variablez. Ce type de polynômes ne peut être associé à un filtre causal mais il se rencontre notamment lorsqu’on étudie le spectre de signaux à temps discret en sortie de filtre à réponse impulsionnelle finie.
Nous commencerons par présenter les propriétés des polynômes de Laurent, puis des matrices polynomiales de Laurent. Nous définirons notamment la L-forme de Smith qui est une extension de la forme de Smith classique, et donnerons une définition précise du degré et l’ordre de ces matrices (notions parfois confondues dans la littérature).
Nous étudierons plus particulièrement les matrices para-hermitiennes et para-unitaires qui sont des matrices respectivement égales à leur matrice para-conjuguée ou dont l’inverse est égale à la para-conjuguée. Nous nous attacherons à développer leurs propriétés particulières en terme de degré notamment, et de factorisation.
Lors de l’étude des systèmes et en traitement du signal, de nombreuses factorisations de matrices à coefficients constants interviennent : factorisa- tions QR (à l’aide d’une matrice orthogonale et d’une matrice triangulaire), LU (à l’aide de deux matrices triangulaires : une inférieure et une supé- rieure), SVD (décompositions en valeurs singulières à l’aide de deux matrices unitaires), EVD (décompositions en valeurs propres-vecteurs propres) [49].
En particulier, le théorème spectral montre que toute matrice hermitienne est diagonalisable à l’aide d’une matrice unitaire, c’est-à-dire que les matrices intervenant dans l’EVD sont des matrices unitaires. La factorisation de Cho- lesky d’une matrice hermitienne définie positive se fait quant à elle à l’aide d’une matrice triangulaire et de sa transposée conjuguée. Ces factorisations ne peuvent pas s’étendre simplement aux matrices polynomiales car les coeffi- cients de ces matrices n’appartiennent pas à un corps mais à un anneau (celui des polynômes de Laurent). De plus, certaines propriétés, comme par exemple la positivité, ne peuvent s’entendre que sur le cercle unité (lorsquez =ejω).
Nous montrerons que dans le cas général, une décomposition EVD dont tous les termes sont polynomiaux pour une matrice para-hermitienne définie po- sitive sur le cercle unité n’existe pas, mais qu’on peut presque-diagonaliser ces matrices à l’aide de matrices para-unitaires continues sur le cercle unité.
Enfin, nous montrerons quel rôle jouent les factorisations des matrices para- unitaires dans l’égalisation aveugle de systèmes convolutifs multivariables, suivant en cela les travaux de McWhriter et al [35, 62, 44].
Curriculum vitæ
Sylvie ICART
née le 6 juin 1965, 2 enfants
Maître de Conférences, 61e section depuis octobre 1991 Laboratoire I3S Informatique Signaux Systèmes, Pôle SIS Polytech’Nice-Sophia Antipolis, Département Electronique
2.1 Formation
– Thèse de doctorat, spécialité Automatique et Informatique Industrielle
«Etude du découplage ligne par ligne avec stabilité : le cas des systèmes linéaires» au Laboratoire d’Automatique de Nantes, juillet 1990, direc- teur de thèse : J.F. Lafay, rapporteurs : J. Descusse (Lan), J.M. Dion (Lag), V. Kucera (Utia Csav), membre : B. Espiau (Inria), mention Très Honorable.
– Dea en Automatique et Informatique Industrielle à l’Ecole Nationale Supérieure de Mécanique de Nantes, «Quelques résultats sur le pro- blème de Morgan», octobre 1987 (mention Bien).
– IngénieurEnsm, spécialité Automatique, juin 1987 (mention Très Bien).
– Classes Préparatoires M’ au lycée Masséna de Nice, 1982-84.
– Baccalauréat série C au lycée Amiral de Grasse, 1982 (mention Très Bien).
2.2 Expérience professionnelle
– Maître de Conférences à l’Université de Nice-Sophia Antipolis : UfrSciences, Département Eea de 1991 à 1999,
Polytech’Nice-Sophia, département Electronique, anciennement Ecole 7
Supérieure d’Ingénieurs de Nice-Sophia Antipolis (Esinsa) depuis 1999.
Membre du Laboratoire I3S depuis 1991.
Congé parental à temps partiel (80%) de septembre 2001 à août 2003.
Congé pour recherches (CRCT) de septembre 2011 à août 2012.
– Boursière post-doctorale à l’Inria Sophia–Antipolis, projet Prisme, Etude de la commande d’un bras de robot flexible, en 1990-91.
– Stagiaire à l’Aérospatiale de Cannes, service Attitude Orbite Contrôle Satellite, découverte du contrôle en entreprise, août 1991.
– Doctorante au LAN, Contrôle de systèmes multivariables, en 1987-90.
– Moniteur de l’Enseignement Supérieur à l’Ensm en 1989-90.
– Vacataire à l’Ensm en électronique et automatique, à l’Iut Geii en automatique et à l’Uer Sciences Economiques en mathématiques de 1987 à 1989.
– Stagiaire au Centre de Mathématiques Appliquées de l’Ecole des Mines de Paris à Sophia-Antipolis : Etude d’une bille sur un plan incliné (2 mois 1/2 en 1986).
2.3 Activités d’Enseignement
Depuis mes débuts en tant qu’enseignant-chercheur, j’ai toujours veillé à enseigner à différents niveaux : du premier cycle au master, en cours, travaux dirigés et travaux pratiques, et à essayer de transmettre à mes étudiants mon enthousiasme pour les mathématiques appliquées à l’ingénierie.
Par exemple, enseigner à des étudiants à bac +1 des outils mathématiques pour l’ingénieur permet de mieux appréhender les acquis de nos étudiants tant d’un point de vue mathématiques que d’un point de vue méthode de travail. En ce qui concerne les travaux pratiques, il me paraît essentiel que les étudiants ne travaillent pas uniquement en simulation avec des logiciels dédiés (tels Matlab ou Scilab) mais également sur des maquettes pédagogiques.
Même si cela est notablement plus exigeant d’un point de vue préparation et entretien, ceci permet aux étudiants de se confronter à des problèmes réels.
Plutôt que de dresser une liste exhaustive des enseignements que j’ai effectués, j’ai choisi d’indiquer les grandes thématiques que j’ai abordées1. La liste des enseignements actuels ainsi que les documents pédagogiques afférents sont disponibles à l’adresse : http ://users.polytech.unice.fr/∼icart.
Mathématiques : Lorsque j’ai été nommée maître de conférences à l’uni- versité de Nice, j’ai eu la responsabilité des cours d’algèbre linéaire de 1ère année à l’Esinsa durant 2 ans (45h Cours, 45hTd). L’école ayant
1. les horaires indiquées sont ceux par étudiant, le nombre de groupes allant de 2 à 8 enTdet de 6 à 10 enTp.
ouvert la même année que celle où j’ai été recrutée, j’ai eu la liberté d’innover en illustrant, par exemple, les notions matricielles sur des exemples physiques concrets.
Toujours dans ce souci de relier mathématiques et ingénierie et suite au travail d’un groupe de réflexion, il a été décidé d’introduire en 1999 un nouveau cours : “Outils Mathématiques pour l’Ingénieur” (OMI) en 1ère année. J’ai participé à l’élaboration du programme de ce cours. J’ai la responsabilité de la partie géométrie de cette matière depuis lors (12h de cours, 12h de Td), et adapte son contenu en fonction des programmes de terminale. En raison de l’augmentation des flux d’étudiants, je n’as- sure plus seule ces enseignements, mais travaille maintenant en équipe avec des vacataires.
Logique et Electronique : Parallèlement à ces enseignements plutôt théoriques, j’ai effectué desTpd’Electronique enEsinsa 1 (utilisation d’oscilloscopes et de GBF, porte ET, OU, diode, multiplexeur, 15h Tp) ainsi que des Tp de logique en Maîtrise Eea (bascules, systèmes synchrones et asynchrones 30h Tp) lorsque j’étais en poste à l’Ufr Sciences.
Traitement du Signal : J’ai tout d’abord eu la responsabilité des cours de Signaux en 2e année deDeug Spi(12h Cours, 12h deTd). Ce cours était orienté sur l’étude des réponses transitoires de systèmes physiques simples à l’aide de la transformée de Laplace.
Lors du renouvellement de la maquette de la maîtrise Eea en 1996, il a été décidé d’introduire le traitement du signal dans ce cursus. J’ai eu la responsabilité de ces Cours, Td etTp en licence (transformée de Fourier, corrélation, spectre, filtrage) puis en maîtrise (filtrage linéaire des signaux déterministes et stochastiques à temps discret). Pour illus- trer les notions de fréquence sur des signaux réels, j’ai choisi de traiter des signaux de parole à l’aide du logiciel Matlab. J’ai effectué ces en- seignements (16h Cours, 16h Td) durant 2 ans, avant ma mutation à l’Esinsa.
Depuis 1999, j’ai la responsabilité des Cours, Td et Tp de Signaux en deuxième année du premier cycle ou PeiP2 (15h Cours, 15h Td, 15h Tp) : systèmes linéaires du premier et du second ordre, notions de filtre passe-haut et passe-bas. Nous traitons également des signaux so- nores. J’assure le cours ainsi qu’une partie des Td etTp et coordonne ces enseignements pour lesquels, suivant les années, interviennent des vacataires, des moniteurs de l’enseignement supérieur (Dcce) ou des Ater (10 groupes de Tp). Depuis que le premier cycle est devenu un Parcours des écoles d’ingénieurs Polytech, les étudiants ne se destinent plus uniquement à l’électronique au sens large, donc même si les théma-
tiques abordées sont les mêmes, la finalité du module est différente. En effet, ce cours d’introduction au traitement du signal et à la théorie des systèmes linéaires ne sera suivi pour la plupart des étudiants d’aucun approfondissement.
Automatique : Après avoir fait des Tp puis des Td et enfin des cours sur les systèmes asservis linéaires continus et les systèmes d’état en maî- triseEea, j’enseigne actuellement l’automatique continue et discrète au département Electronique de Polytech’Nice-Sophia.
En 1ère année de cycle ingénieur (Elec3), je participe auxTd(23hTd) et ai la responsabilité des Tp (16.5h Tp, 6 groupes). Comme indiqué dans le préambule, les Tp d’asservissement s’effectuent sur des ma- quettes pédagogiques. Les étudiants peuvent ainsi se rendre compte que l’automatique “ce n’est pas que des maths”, voir la différence entre si- mulation et réalité, et appréhender les limites entre théorie et pratique.
J’effectue ces enseignements pour moitié avec des Ater qui changent chaque année.
En Elec4, j’ai la responsabilité des cours et Td d’Automatique (23h Cours, 23h Td) : lois de commande par retour d’état, correcteurs nu- mériques à avance et retard de phase, PID. J’ai également eu la res- ponsabilité des Tp d’Automatique en Elec4 durant plusieurs années (1999-2007).
Depuis 2009, j’assure la mise à niveau en automatique d’étudiants chi- nois en programme Mundus au niveau bac+3. Ces cours de 20 heures sont une nouvelle expérience pédagogique car les étudiants n’ont ni la même culture scientifique ni les mêmes méthodes de travail que nos étudiants habituels.
Les étudiants au département Electronique n’ont pas vocation à de- venir des spécialistes de l’automatique. Le but de cet enseignement est qu’ils puissent en appréhender les notions fondamentales (boucle ouverte, boucle fermée, contre-réaction, problème de stabilité, interac- tions entre analogique et numérique. . .) et qu’ils soient aptes à saisir les problématiques associées, ce que j’ai pu observer notamment lors de leurs stages de fin d’études.
Systèmes multivariables : L’étude des systèmes multivariables ne se fait qu’au niveau Master 2 puisque c’est à la fois un problème com- pliqué et pointu. C’est pourquoi je l’ai enseigné en Dea Aravis, puis au Master Sicom (15h Cours durant 6 ans). L’étude de ces systèmes est illustrée par des problèmes d’automatique (commande) mais éga- lement de télécommunications lorsque plusieurs émetteurs et plusieurs récepteurs travaillent simultanément : il s’agit alors d’égalisation multi- variable. Ce dernier point était en phase avec mes travaux de recherche
actuels. Depuis la refonte des masters en 2007, l’étude des systèmes multivariables n’est plus enseignée localement.
Activités pédagogiques annexes : Enfin, je participe régulièrement aux Journées Portes Ouvertes ainsi qu’au Sophia Forum et aux en- tretiens Polytech qui nous permettent de recruter nos futurs étudiants.
J’encadre aussi tous les ans des stagiaires en entreprise au niveau tech- nicien ou ingénieurs (3 à 6 par an).
2.4 Fonctions d’intérêt collectif
Avant de détailler les fonctions d’intérêt collectif auxquelles j’ai consacré beaucoup de temps et d’énergie, voici, par ordre chronologique, la liste des fonctions d’intérêt collectif qui m’ont été confiées ou pour lesquelles j’ai été élue, au sein du laboratoire, de l’école ou de l’université :
– Membre du conseil du laboratoire I3S de février 93 à septembre 94.
– Membre suppléante de la commission de spécialistes 61e section de l’UNS de 1998 à 2002.
– Responsable des stages techniciens au Département Electronique de Polytech’Nice-Sophia d’octobre 1999 à juin 2009.
– Coresponsable de l’option Traitement Numérique du signal au Dépar- tement Electronique de Polytech de 2000 à 2003.
– Membre titulaire de la commission de spécialistes 61e section de sep- tembre 2002 à juillet 2008.
– Membre suppléant du Comité des Projets de l’I3S de 2003 à 2005.
– Assesseur de la commission de spécialistes 61e section, mars 2005 à juillet 2008 (fin des CS).
– Membre du Conseil d’Ecole de Polytech de 2005 à 2010.
– Membre du jury du concours ITRF session 2006 niveau Ingenieur BAP Electronicien.
– Responsable de l’option TNS de 2006 à 2009.
– Membre du Conseil du Département Réseaux et Télécom de l’IutNice Côte d’Azur de 2007 à 2011.
– Responsable des stages de fin d’études au Département Electronique depuis juin 2009.
– Membre du vivier de la section 61 de l’université de Nice-Sophia Anti- polis depuis février 2009.
– Membre du Comité de Sélection du poste MCF n°184, EPU Nice-Sophia Antipolis, avril-mai 2009.
– Membre du Comité de Sélection du poste MCF n°167, Iut GEII Nice, mai 2011.
– Membre du Conseil de Département Electronique de Polytech’Nice- Sophia depuis juin 2011.
Responsabilité des Stages Techniciens (1999-2009)
Les stages techniciens concernent 70 étudiants. D’une durée de 8 semaines minimum, ils ont lieu en fin d’Elec4. La responsabilité des stages est un mélange de travail administratif (établissement des conventions, envoi et suivi des conventions), de contact avec le milieu d’accueil (évaluation des stages), de suivi pédagogique (validation des stages) et d’organisation (choix des jurys de soutenance, répartition des rapports de stage aux relecteurs, planning des jurys et enfin compilation des notes données par les entreprises, les relecteurs et le jury de soutenance). Pendant les 10 années où j’ai été responsable de ces stages, nous ne disposions au département Electronique d’aucun support administratif, c’était donc une activité très chronophage.
Le stage technicien est une étape importante dans la vie de nos étudiants.
Leur premier stage, ou stage ouvrier, se fait majoritairement dans un domaine fort éloigné de l’électronique. Pour beaucoup de nos élève-ingénieurs, le stage technicien est donc le premier contact avec le milieu industriel dans lequel ils évolueront durant leur future carrière. C’est aussi pour les enseignants, un indicateur des tendances actuelles et un outil leur permettant de faire évoluer le contenu des enseignements, notamment via les exemples d’application.
Responsabilité de l’option TNS (2006-09)
L’option TNS au département Elec s’étend sur 2 semestres (plus un se- mestre de stage). La responsabilité consiste en l’établissement des emplois du temps, en la recherche d’intervenants académiques et industriels (plus d’une vingtaine) et à la coordination des différents enseignements. Enfin, il faut adapter les maquettes pédagogiques afin de coller au mieux à cette spécialité en constante évolution.
Nous avions également un partenariat privilégié avec la société Texas Instrument, je m’occupais du Prix Texas ainsi que de l’organisation de la ren- contre annuelle du programme Elite de TI qui s’adressait à tous les enseignants- chercheurs du domaine à l’UNS (Iut, UfrSciences, Polytech).
Parallèlement, et à cause d’un réel sous-encadrement, je m’occupais de recenser tous les enseignements et intervenants en automatique et traitement du signal au département ainsi qu’en premier cycle. Ceci a conduit notam- ment à l’établissement d’une fiche de poste d’un professeur en 61e section (poste pourvu en janv. 2009) et à celle d’un poste de maître de conférences (poste pourvu en sept. 2009).
Responsabilité des stages de fin d’études (2009-)
Depuis septembre 2009, j’ai pris la responsabilité des stages de fin d’études au département Electronique. Ces stages d’une durée de 6 mois concernent une soixantaine d’étudiants.
Comme pour les stages techniciens, cette responsabilité est multiple mais s’étend sur une plus grande partie de l’année universitaire : jurys, plannings, diffusion des offres de stage, conseils aux étudiants, affectation des tuteurs, conventions, relations avec les entreprises afin de pérenniser les accueils de stagiaires. En parallèle, je m’occupe du devenir des étudiants nouvellement diplômés. Concernant la partie administrative, nous bénéficions depuis 2 ans d’une assistante à temps partiel, ce qui a allégé mon travail purement ad- ministratif. De plus, grâce à notre expérience, j’ai pu établir un cahier des charges puis testé la gestion des conventions en ligne. Le site est mainte- nant opérationnel et est utilisé depuis 2 ans par tous les départements de Polytech (http ://conventions.polytech.unice.fr/). J’utilise également la pla- teforme Jalon de l’université pour gérer les dépôts en ligne des stages.
L’importance des stages de fin d’études au sein d’une école d’ingénieurs n’est plus à démontrer. La mutation de nos étudiants d’élèves en ingénieurs grâce à leurs acquis, leur travail et leur capacité à mener à bien un projet est le but d’une formation. Les relations que nous tissons avec les entreprises et les laboratoires lors de ces stages sont essentielles. Elles nous permettent d’adapter le contenu des enseignements via une forte interaction entre le responsable des stages, les responsables d’option et les maîtres de stage en entreprise.
2.5 Activités de Recherche
Le point commun de tous mes travaux de recherche est l’utilisation de l’algèbre linéaire avec une emphase particulière sur les méthodes utilisant des matrices polynomiales. Dans cette partie, les références citées sont celles dont je suis co-auteur.
Après avoir fait de la commande multivariable en thèse [1, 5, 6, 7, 27, 28], puis de l’automatique pour la robotique en post-doctorat [29, 8], je me suis orientée vers le traitement du signal et l’égalisation multivariable.
J’ai participé à l’encadrement de la thèse d’Olivier Lemoine, dirigée par Gérard Alengrin et soutenue en octobre 1995 sur la détection de signaux non stationnaires par représentation temps-fréquence [9, 10].
La participation au Gdr Traitement du Signal [30] m’a fait découvrir un nouvel axe de recherche : l’égalisation aveugle multicapteurs, c’est-à-dire
de systèmes pour lesquels on ne dispose pas de séquence d’apprentissage pour l’identification mais dont on connaît les propriétés statistiques. J’ai ainsi encadré seule deux stages de Dea. Roland Gautier a travaillé sur la séparation de mélanges convolutifs de février à juillet 1995 ; ce travail a donné lieu à une publication à ICASSP’96 [11]. Le stage de Dea de Ansi Ansori portait quant à lui sur la simulation d’une chaîne de communication à l’aide du logiciel Matlab, de février à juin 1996.
Parallèlement, dans notre groupe de travail local, nous nous sommes inté- ressés aux problèmes d’égalisation de systèmes monovariables lorsque l’erreur est bornée (ce qui est une hypothèse tout à fait réaliste !), en tenant compte du caractère fini de l’alphabet [12, 13].
Puis, nous avons travaillé avec Joël LeRoux sur l’égalisation de systèmes à l’aide d’un critère exprimé dans le domaine spectral et applicable à des signaux complexes [14].
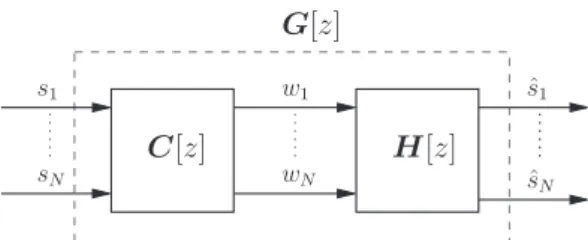
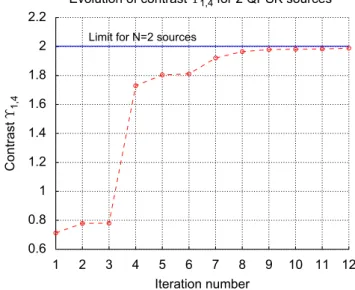
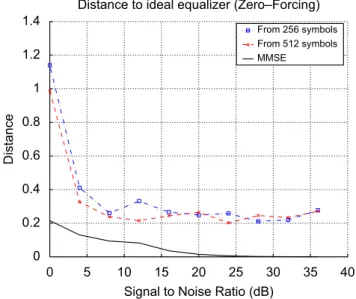
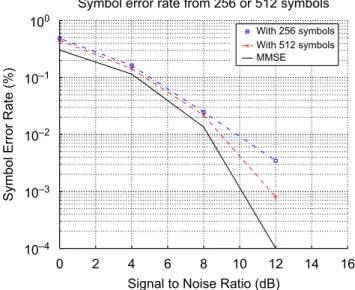
J’ai ensuite co-dirigé avec Pierre Comon la thèse de Ludwig Rota : «Ega- lisation aveugle de systèmes multi-utilisateurs» (soutenue le 15 décembre 2004). Les systèmes étudiés comportent plusieurs émetteurs et plusieurs cap- teurs. Les signaux émis sont supposés inconnus mais indépendants. Le ca- nal de transmission est linéaire stationnaire invariant dans le temps et à réponse impulsionnelle finie : sa matrice de transfert est alors une matrice polynomiale. Si les observations sont blanchies, cette matrice est de plus para- unitaire. Nous nous servons des propriétés des matrices para-unitaires et d’un critère de constraste basé sur les statistiques d’ordre supérieur à deux des ob- servations pour construire un égaliseur permettant de retrouver les sources.
Ces travaux ont donné lieu à trois communications dans des conférences in- ternationales [17, 15, 16]. L’extension des derniers résultats est parue en mars 2009 dans la revue Signal Processing [2].
De février 2007 à juin 2010, j’ai co-encadré avec Luc Deneire et Lieven De Lathauwer (de l’université de Louvain en Belgique) la thèse de Mikael Sorensen dans le cadre du programme européen Marie Curie Est Signal :
«Tensor Tools with Application in Signal Processing», thèse soutenue le 14 juin 2010. Ces travaux portent sur la diagonalisation de tenseurs et le pro- blème se pose différemment selon que l’on a des tenseurs symétriques ou non.
En effet, l’utilisation des moments d’ordre supérieur à deux pour l’étude des systèmes multivariables, fait intervenir non plus seulement des matrices mais également des tenseurs (algèbre multilinéaire). Les compétences en algèbre multilinéaire de plusieurs chercheurs au sein de l’équipe Signal de l’I3S nous ont permis de mener à bien des études pointues sur ce sujet. Ces travaux ont donné lieu à trois communications dans des conférences internationales [18, 19, 20] ainsi qu’à un article dans la revue Signal Processing [4] et un à paraître dans SIMAX [3].
Actuellement, j’étudie plus particulièrement les propriétés structurelles des matrices polynomiales de Laurent. Ce travail a donné lieu à un article de conférence [21] et va être développé dans les sections suivantes.
Enfin, je suis assez régulièrement relectrice pour des conférences (ICASSP, ITS, ICC, EUSIPCO) ou des revues (Automatica, IEEE Transaction on Si- gnal Processing, Signal Processing, International Journal of Adaptive Control and Signal Processing, Springer Signal Image and Video Processing).
Encadrements et jurys
Encadrement
– Thèse O. Lemoine «Détection de signaux non stationnaires par re- présentation temps-fréquence», dirigée par G. Alengrin, octobre 1995 (30%).
– Dea R. Gautier : «Séparation de mélanges convolutifs», juillet 1995 (100%).
– DeaA. Ansori «Simulation d’une chaîne de communication à l’aide du logiciel Matlab», juin 1996 (100%).
– Thèse L. Rota «Egalisation aveugle de systèmes multi-utilisateurs», décembre 2004, co-direction avec P. Comon (50%).
– Thèse M. Sorensen «Tensor Tools with Application in Signal Proces- sing», juin 2010, co-direction avec L. Deneire et L. De Lathauwer (30%).
O. Lemoine est actuellement chef de projets à Thalès, R. Gautier maître de conférences à Brest, L. Rota ingénieur d’études chez Orange Business Services et M. Sorensen est en post-doctorat à U.K. Leuven.
Participation à des jurys de thèse
– Ludwig Rota «Egalisation aveugle de systèmes multi-utilisateurs», 15 décembre 2004.
– Mikael Sorensen «Tensor Tools with Application in Signal Processing», le 14 juin 2010.
– Thomas Bouilloc «Applications de décompositions tensorielles à l’iden- tification de modèles de Volterra et aux systèmes de communication MIMO-CDMA», 9 Décembre 2011.
Publications
La liste de mes publications se trouve en page 61.
Matrices L-polynomiales et égalisation
Comme indiqué précédemment, nous allons plus particulièrement déve- lopper dans ce mémoire les résultats de nos derniers travaux sur les ma- trices polynomiales de Laurent, appelées encore matrices L-polynomiales et leur application en égalisation aveugle multivariable. Nous ferons d’abord des rappels sur les polynômes de Laurent puis exposerons différentes propriétés des matrices polynomiales de Laurent notamment en terme de décomposition et de factorisation. Les notions d’hermitianité et d’unitarité s’étendent aux matrices polynomiales, on parle alors de matrice para-hermitienne et de ma- trice para-unitaire ; mais les décompositions en valeurs singulières (PSVD) ou en valeurs-propres, vecteurs propres (PEVD) ne peuvent s’étendre car les éléments des matrices considérées n’appartiennent pas à un corps. Nous mon- trerons cependant que l’on peut approximer de telles décompositions à l’aide de fonctions continues sur le cercle unité, sans toutefois pouvoir imposer aux différents facteurs d’être polynomiaux.
Enfin, nous montrerons quel rôle jouent les matrices para-unitaires et para-hermitiennes dans l’égalisation aveugle de mélanges convolutifs à ré- ponse impulsionnelle finie.1
3.1 Polynômes de Laurent
Les notations et dénominations sur les polynômes diffèrent d’un ouvrage à l’autre et suivant le domaine d’application considéré. Dans cette partie, nous présentons les notations et définitions utilisées dans la suite de ce document
1. On aurait pu commencer par le problème qui a motivé ces travaux, mais il aurait fallu pour cela introduire de nombreuses notations qui nuiraient à la lecture.
17
et qui seront utiles pour l’études des matrices polynomiales de Laurent. Une annexe page 69 présente les autres définitions rencontrées dans la littérature.
3.1.1 Notations
On noteC[z]l’anneau des polynômes2en l’indéterminéez et à coefficients dans C :
p(z)∈C[z] ssi p(z) = Xn
i=0
pizi avec n∈N, pi ∈C
Le degré de p est noté deg(p) et correspond au plus grand entier i tel que pi 6= 0.
On note Cs[z] l’ensemble des polynômes dont les racines sont toutes de module strictement inférieur à 1, ces polynômes sont à minimum de phase strict.
On note C[z−1] l’anneau des polynômes en l’indéterminéez−1 et à coeffi- cients dansC :
p(z)∈C[z−1] ssip(z) = Xn
i=0
piz−i avecn ∈N, pi ∈C
Le degré de p est aussi noté deg(p) et correspond au plus grand entier i tel quepi 6= 0.
On noteC[z, z−1]l’anneau des polynômes de Laurent en l’indéterminéez c’est à dire des polynômes ayant des puissances positives et négatives de z :
p(z)∈C[z, z−1] ssip(z) = Xn i=m
pizi avecm, n∈Z, pi ∈C. On appellera par la suite ces polynômes des L-polynômes.
3.1.2 Propriétés et définitions
Propriété 1. L’ensemble des polynômes de Laurent (C[z, z−1],+, .) est un anneau intègre.
(C[z, z−1],+) est un groupe commutatif : + est une loi interne, commu- tative, associative, l’élément neutre est le polynôme nul, l’opposé dep(z)est
−p(z).
2. par souci de clarté, nous noterons la plupart du temps un polynôme en faisant apparaître explicitement la variable associée, c’est à dire on notera le polynômepcomme p(z), p(z−1)est alors la fonction obtenue en substituantz parz−1.
La multiplication est associative et possède un élément neutre p(z) = z0 = 1, elle est distributive par rapport à l’addition, il n’y a pas de diviseur de zéro donc(C[z, z−1],+, .) est un anneau intègre.
L’ensemble de ses éléments inversibles (qui est donc un groupe commu- tatif) est défini par U = {p(z) ∈ C[z, z−1], p(z) = azα aveca ∈ C∗, α ∈ Z}, ce sont des monômes.
Deux L-polynômes sont associés s’ils sont égaux à une multiplication par un élément de U près. Comme pour un polynôme “classique” auquel on peut associer un polynôme unitaire (ou monique c’est à dire dont le coefficient du terme de plus haut degré est égal à 1) on peut associer à tout L-polynôme un polynôme L-unitaire :
Définition 2. On dira qu’un polynôme est L-unitaire s’il est unitaire et qu’il n’admet pas zéro comme racine.
Soit p(z) ∈ C[z, z−1], posons p(z) = Pn
i=mpizi avecpi ∈ C, m, n ∈ Z, m≤n, pm et pn non nuls. On peut donc factoriser
p(z) = pnzmPn i=m
pi
pnzi−m = pnzmPn−m
i=0 πizi = pnzmπ(z) avec π(z) ∈ C[z]
et L-unitaire car par définition π0 = ppm
n 6= 0 et πn−m = ppn
n = 1. Notons que le polynômeπ associé à painsi défini est unique.
Pour montrer que l’anneau des polynômes de Laurent est euclidien, on a besoin de définir un stathmed, c’est à dire une application deC[z, z−1]\ {0} dans N telle que d(pq) ≤ d(p)d(q) pour tout L-polynômes p, q non nuls et auquel on peut associer une division euclidienne.
Définition 3. Soit p(z) ∈ C[z, z−1], p(z) = Pn
i=mpizi avec pi ∈ C, m, n ∈ Z, m≤n, pm et pn non nuls. Posons
p(z) =pnzmπ(z) (3.1)
π(z)∈C[z]est un polynôme de degrén−m(≥0par définition). On appellera L-degré d’un L-polynôme p le degré du polynôme associé π, on notera ce L- degré d(p).
Notons que la multiplication par un monôme ne modifie pas le degré ainsi défini et que le L-degré ne coïncide pas avec le degré lorsqu’on est sur C[z] : par exemplep(z) = z2+z4 =z2(1+z2)a un degré 4 surC[z]mais un L-degré de 2.
Enfin, pour un polynôme p appartenant à C[z], on a deg(p) ≥d(p) avec égalité ssi z = 0 n’est pas racine de p. Soit p ∈ C[z] tel que deg(p) = n, on peut donc écrire :
• p(z) =z0Pn
i=0pizi avecp0 6= 0si 0 n’est pas racine dep, par définition du L-degré on a donc d(p) =n= deg(p)
• si 0 est racine de p, alors on écrit p(z) = zmπ(z) avec π qui n’admet pas de racine en 0. On a alorsdeg(p) =m+ deg(π) =m+d(p)d’après la définition du L-degré.
Remarque : le L-degré ainsi défini est identique à l’ordre effectif utilisé en Télécom, notamment par McWhriter [44].
Propriété 4. (C[z, z−1],+, .) est un anneau euclidien.
Soient a(z) et b(z) deux L-polynômes quelconques avec b 6= 0. Montrons qu’il existe deux L-polynômes q(z) etr(z) tels que
a(z) = b(z)q(z) +r(z)avec r= 0 oud(r)< d(b)
Posonsa(z) = zmaα(z),α(z)∈C[z],deg(α) =d(a), etb(z) =zmbβ(z), β(z)∈ C[z], deg(β) = d(b).
C[z]étant un anneau euclidien, on peut faire la division euclidienne deα par β :
∃ κ, ρ∈C[z]tq α(z) = β(z)κ(z) +ρ(z), ρ= 0 ou deg(ρ)<deg(β) Par définition deα et β, on a donc :
z−maa(z) =z−mbb(z)κ(z) +ρ(z), soit a(z) =b(z){zma−mbκ(z)}+zmaρ(z) zma−mbκ(z)etzmaρ(z)sont des L-polynômes etd(zmaρ(z)) =d(ρ)par défini- tion du L-degré. Si ρest non nul, d(b) = deg(β)>deg(ρ)≥d(ρ). En posant q(z) =zma−mbκ(z)etr(z) =zmaρ(z), on obtient bien la division euclidienne dea par b, avec d(r)< d(b). Si ρ= 0 alors on a r= 0.
Rappelons qu’un idéal I d’un anneau R est un sous groupe additif tel que∀x ∈ R et y∈ I, xy∈ I etyx ∈ I. Il est principal s’il peut-être généré par un seul élément.
C[z, z−1] étant euclidien, il est principal (principal ideal domain PID).
Comme l’anneau est principal on peut définir les notions de plus grand com- mun diviseur (pgcd) et de plus petit commun multiple (ppcm) d’une famille de L-polynômes. Un plus grand diviseur n’étant défini qu’à une multiplication par un élément inversible près, on imposera à ce pgcd d’être L-normalisé : Définition 5. Soit {p1, . . . , pn} une famille d’éléments de C[z, z−1]. On ap- pelle plus grand diviseur commun des pi le polynôme p∈C[z]tel que pdivise pi pour tout i et p est L-unitaire.
Propriété 6. (C[z, z−1],+, .) est une algèbre sur C.
Cette propriété est évidente : si p(z) et q(z) sont des L-polynômes et a etb sont des nombres complexes,ap(z) est un L-polynôme,a(p(z) +q(z)) = ap(z) + aq(z), (a + b)p(z) = ap(z) + bp(z), a(bp(z)) = (ab)p(z) et enfin 1p(z) = p(z).
Définition 7. Soitp(z)∈C[z, z−1]un L-polynôme, le polynôme para-conjugué de p(z) est le L-polynôme p(z)e ∈C[z, z−1] défini3 par
e
p(z) = p∗(1
z∗),∀z ∈C∗
La para-conjugaison est une involution sur l’algèbre(C[z, z−1],+, .)puisque pour tous L-polynômes p, p1, p2 on aeep=p, p^1+p2 =pe1+pe2,pg1p2 =pe2pe1 et
∀λ∈C,fλp=λ∗p.e
Lorsqu’on se restreint au cercle unité, c’est à dire si z =eω, ω∈R, alors
1
z∗ =z etp(ee ω) =p∗(eω). En particulier, p(eω)p(ee ω) = |p(eω)|2 ∈R+,∀ω.
Remarquons que si p(z)∈C[z] alors p(z)e ∈C[z−1].
Propriété 8. Le L-degré est identique pour un L-polynôme et son para- conjugué.
Soit p(z) = Pn
i=mpizi, pm et pn non nuls, m ≤ n, alors par définition e
p(z) =Pn
i=mp∗iz−i =z−nPn
i=mp∗izn−i, soit en faisant le changement d’indice l = n−i, p(z) =e z−nPn−m
l=0 p∗n−lzl. p∗n et p∗m étant non nuls par hypothèse, le L-degré de p(z)e est égal à n −m qui est aussi par définition le L-degré de p. Cette démonstration vaut pour m, n ∈ N ou Z, c’est à dire pour un polynôme ou un polynôme de Laurent.
Remarquons enfin que le polynôme γ(z)associé au polynôme para-conju- gué ep(z)dep(z)est le polynôme réciproque du polynômeπ(z)associé àp(z) c’est-à-dire que π(z) et γ(z) sont des polynômes de même degré (n − m) vérifiant γ(z) =zn−meπ(z).
En effet, posons p(z) = Pn
i=mpizi = zmPn−m
i=0 πizi avec πi = pi+m. On a e
p(z) =z−nPn−m
l=0 p∗n−lzl=z−nPn−m
l=0 γlzl, soit γl =p∗n−l.
π(z) étant un polynôme de degré n−m, son polynôme réciproque est π∗(z) = zn−mπ(z) =e zn−mπ∗(z1∗) = zn−mPn−m
i=0 π∗iz−i = Pn−m
i=0 πi∗zn−m−i = Pn−m
i=0 p∗i+mzn−m−i, soit en faisant le changement d’indice l = n − m− i, π∗(z) =zn−mPn−m
l=0 p∗n−lzl, soit π∗(z) =γ(z).
Si π(z) et γ(z) sont définis comme les polynômes L-unitaires associés à p(z)et p(z), la relation est un peu plus complexe : on ae p∗mγ(z) = p∗nπ∗(z).
3. lorsquep(z)∈C[z], on trouve également une définition différente pour que le poly- nôme para-conjugué soit aussi un polynôme appartenant àC[z], cf Annexe page 69.
Définition 9. Soit p un L-polynôme, on dira que p est para-hermitien ssi il est égal à son para-conjugué, c’est à dire p=peou encore p(z) = p∗(z1∗) ∀z ∈ C∗.
Propriété 10.Sipest un L-polynôme para-hermitien, alorsp(z) =Pd
i=−dpizi avec p−i =p∗i, et le L-degré de p est pair.
Soit p(z) = Pn
i=mpizi, pm et pn non nuls, alors p(z) =e Pn
i=mp∗iz−i = P−m
i=−np∗−izi, d’où pour avoir égalité des polynômes n = −m et p−i = p∗i pour i = 1 à n et p0 = p∗0. Il suffit ensuite d’écrire p(z) = z−dP2d
i=0pi−dzi pour avoir le L-degré égal à2d.
Les polynômes para-hermitiens vérifient également la propriété suivante, également connue sous le nom de Théorème de Fejér-Riesz :
Propriété 11. Soit p(z) un L-polynôme para-hermitien strictement positif sur le cercle alors on peut factoriser [75] :
p(z) = l(z)el(z) avec l(z)∈Cs[z] à minimum de phase strict.
Remarquons tout d’abord qu’un polynôme para-hermitien a toujours une valeur réelle sur le cercle, puisque p(ee ω) = p∗(eω). De plus, les zéros d’un polynôme para-hermitien sont symétriques par rapport au cercle unité : si z0 est zéro de p(z), alors z1∗
0 est également zéro de p(z). En effet, comme p(z) = p(z), on ae p(z0) = 0 = p∗(z1∗
0), soit p(z1∗
0) = 0. Supposons de plus que ce polynôme est strictement positif sur le cercle, c’est à direp(eω)>0∀ω, ce qui implique, en particulier, que p(z) n’a pas de racine sur le cercle. Posons p(z) = αQd
i=1(1−a−1i z)(1−a−1∗i z−1), où lesai sont les zéros à l’intérieur du cercle unité.p(eω) = αQd
i=1|1−a−1i eω|2 >0implique que αest un nombre réel positif. En posant l(z) = √
αQd
i=1(1−a−i 1z), on a immédiatement la factorisation désirée.
Définition 12. Soit p un L-polynôme, on dira que p est para-unitaire ssi p(z)p(z) = 1e ∀z ∈C∗. On a p(z) = eθzα, θ ∈R, α∈Z.
D’après leur définition, les L-polynômes para-unitaires sont des éléments inversibles de l’anneau des L-polynômes, ce sont donc des monômes. Pour quep(z)p(z) = 1, il faut de plus que la constante du monôme soit de modulee 1, soit,p(z) est para-unitaire ssi p(z) =eθzα, θ∈R, α∈Z.
Propriété 13. L’algèbre des polynômes de Laurent sur le cercle unité et à valeurs dansCest dense dans l’ensemble des fonctions continues sur le cercle à valeurs dans C.
Soit A l’algèbre des polynômes de Laurent sur le cercle unité C à valeurs dans C :
A={p:C →C tq p(z) = Xn i=m
pizi avec m, n∈Z, pi ∈C et|z|= 1} Sur le cercle, z1∗ =z et donc si p(z) ∈ A,p(z)e ∈ A, soit A est auto-adjoint.
De plus, A sépare les points du cercle, c’est à dire que ∀x, y ∈ C il existe p(z) ∈ A tel que p(x) 6= p(y). Enfin, le cercle unité est un espace métrique compact. D’après le théorème de Stone-Weierstrass, on peut donc en déduire queA est dense dans l’ensemble des fonctions continues deC à valeurs dans C pour la norme infinie ||f||= supx∈C|f(x)|.
Toute fonction continue et 2π-périodique sur R à valeurs dans C peut donc être approchée par des polynômes trigonométriques.
3.2 Matrices polynomiales de Laurent
L’anneau des polynômes de Laurent (C[z, z−1],+, .) n’est pas un corps car tous ses éléments ne sont pas inversibles donc l’ensemble des tableaux à n lignes et une colonne dont les entrées (composantes) sont des éléments deC[z, z−1] n’est pas un espace vectoriel mais un module sur C[z, z−1]. Cet ensemble est notéCn[z, z−1]et ses élémentsv(z). Par abus de langage, et pour simplifier la lecture, nous appellerons toutefois ces éléments des vecteurs L- polynomiaux.
Remarquons enfin que l’ensemble des tableaux v(z)∈Cn[z, z−1]dont les composantes sont des L-polynômes para-hermitiens est un-sous groupe de Cn[z, z−1] mais pas un sous-module (car le produit d’un L-polynôme quel- conque par un L-polynôme para-hermitien n’est pas para-hermitien).
L’ensemble des matrices n×n dont les entrées sont des L-polynômes est un anneau noté Cn×n[z, z−1]. Ses éléments sont appelés des matrices poly- nomiales de Laurent ou encore matrices L-polynomiales. Cn×n[z] est quant à lui l’anneau des matrices dont les composantes sont des éléments de C[z], c’est à dire des matrice polynomiales “classiques“.
Définition 14. Les éléments inversibles de l’anneau des matrices L-polyno- miales Cn×n[z, z−1] sont appelés matrices L-unimodulaires, ce sont des ma- trices dont le déterminant est un élément deU, c’est à dire un monôme non nul.
Comme pour les matrices polynomiales, on peut définir des opérations élémentaires sur les matrices polynomiales de Laurent : multiplier une ligne (resp. une colonne) par un L-polynôme non nul, échanger deux lignes (resp.
colonnes), ajouter à une ligne (resp. colonne) le produit d’une autre ligne (resp. colonne) par un L-polynôme. Ces opérations élémentaires sur les lignes correspondent à des multiplications à gauche par une matrice L-unimodulaire et celles sur les colonnes à une multiplication à droite par une matrice L- unimodulaire.
3.2.1 Forme de Smith des matrices polynomiales de Laurent
Comme l’anneau des polynômes de Laurent est un anneau principal, on peut définir la forme de Smith normale [36] d’une matrice à coefficients dans C[z, z−1].
Définition 15. Soit M(z)∈ Cn×n[z, z−1], alors il existe U1(z) et U2(z) ∈ Cn×n[z, z−1] L-unimodulaires telles que
U1(z)M(z)U2(z) =Λ(z)
Λ(z) =
λ1(z) . ..
λr(z) 0
0 0
• λi(z) uniques à une multiplication par un monôme près
• λi(z) divise λi+1(z).
• r est le rang (normal) de la matrice M(z).
Λ(z) est appelée forme normale de Smith de M(z), les λi(z) sont appelés facteurs invariants ou diviseurs élémentaires.
Afin de définir ces facteurs invariants de manière unique, on va leur im- poser, comme pour les pgcd, d’être L-unitaires.
Définition 16. Soit M(z) ∈Cn×n[z, z−1]. On appelle L-forme de Smith de M(z) la matrice polynomiale diagonale Λ(z)∈Cn×n[z] telle que
U1(z)M(z)U2(z) =Λ(z)
où U1(z) et U2(z)∈Cn×n[z, z−1] sont L-unimodulaires et
Λ(z) =
µ1(z) . ..
µr(z) 0
0 0
avec µi(z) divise µi+1(z) et est L-unitaire.
Les µi(z)∈C[z] sont appelés L-polynômes invariants de M(z).
Sur l’anneau des matrices polynomiales “classiques“ Cn×n[z], il existe une forme de Smith bien connue [54] qui fait intervenir des matrices unimodulaires dont le déterminant est une constante non nulle. Dans le cas d’une matrice carrée de rang plein, on a le résultat suivant :
Soit M(z) ∈ Cn×n[z], alors ∃V1(z) et V2(z) ∈ Cn×n[z] unimodulaires telles que
V1(z)M(z)V2(z) = diag{λi(z)}
les λi(z) sont les polynômes invariants de M(z), ils sont uniques si on les suppose normalisés (monic) et vérifient λi(z) divise λi+1(z). La matrice diag{λi(z)} est appelée forme de Smith de M(z).
Il est facile de montrer que si M(z)∈Cn×n[z]les L-polynômes invariants coïncident avec les polynômes invariants lorsque zéro n’est pas racine de ces polynômes.
Propriété 17. Si M(z) est une matrice L-polynomiale de rang plein, alors son déterminant est à une multiplication par un monôme près, le produit de ses L-polynômes invariants.
Par définition de la L-forme de Smith deM(z), on a detΛ(z) =Y
i
µi(z) = detU1(z) detM(z) detU2(z) avecdetUi(z) qui sont des monômes car lesUi sont L-unimodulaires.
On peut définir l’équivalence au sens de Smith de deux matrices L- polynomiales :
Définition 18. Soient M(z) et P(z) ∈Cn×n[z, z−1], alors M(z) LS∼ P(z), ssi elles ont même L-forme de Smith, c’est à dire ssi il existe U1(z)etU2(z) L-unimodulaires telles que
M(z) =U1(z)P(z)U2(z)
Pour éviter la confusion avec l’équivalence au sens de Smith “classique“
(ie à des matrices unimodulaires près), on appellera cette équivalence, l’équi- valence au sens de L-Smith ou L-équivalence au sens de Smith afin de rap- peler que les égalités ont lieu à des matrices polynomiales de Laurent L- unimodulaires près.
Propriété 19. Les matrices L-unimodulaires sont L-équivalentes au sens de Smith à la matrice identité.
En effet, le déterminant d’une matrice L-unimodulaire est égal à un mo- nôme, mais aussi au produit de ses L-polynômes invariants et d’un mo- nôme. Donc, ces L-polynômes sont des monômes, mais par définition, les L-polynômes invariants sont L-unitaires, ils ne peuvent donc être égaux qu’à 1 : µi(z) = 1,∀z.
Propriété 20. Si deux matrices sont L-équivalentes au sens de Smith, alors les pgcd des mineurs d’ordre j de ces matrices sont égaux.
Soient A(z) et B(z) ∈ Cn×n[z, z−1] telles que A(z) LS∼ B(z), il existe U(z) et V(z) L-unimodulaires telles que B(z) = U(z)A(z)V(z). Soit b(z) un mineur d’ordre j de B(z), d’après le formule de Binet-Cauchy, on a :
b(z) =X
i
ui(z)ai(z)vi(z) (3.2) oùui, ai, vi sont des mineurs d’ordrej deU, A etV.
Soit ∆j(z)le pgcd de tous les mineurs d’ordrej deA. D’après la relation (3.2),∆j(z)diviseb(z)et ceci quelque soit le mineur d’ordrej deB(z), donc
∆j(z)divise le pgcd des mineurs d’ordrejdeB(z)que l’on va noterδj(z). En écrivant maintenantA(z) =U−1(z)B(z)V−1(z), par le même raisonnement, on peut en déduire que δj(z) divise∆j(z). Ces polynômes étant L-unitaires, on peut en déduire qu’ils sont égaux.
Propriété 21. Soit M(z)∈Cn×n[z, z−1] une matrice L-polynomiale, soient µi(z) ses L-polynômes invariants. Soit ∆j(z) le pgcd des mineurs d’ordre j de M(z), alors
µj(z) = ∆j(z)
∆j−1(z)
D’après la propriété 20, le pgcd des mineurs d’ordre j de M(z) est égal au pgcd des mineurs d’ordre j de sa L-forme de Smith Λ(z). Λ(z) étant une matrice diagonale telle que µi(z) divise µi+1(z), le pgcd des mineurs d’ordre j de Λ(z) est Qj
i=1µi(z), soit ∆j(z) = Qj
i=1µi(z) et de même,
∆j−1(z) = Qj−1
i=1 µi(z) d’où ∆j(z) = ∆j−1(z)µj(z). Là encore, tous les po- lynômes considérés sont L-unitaires et n’admettent donc aucun zéro en zéro ou l’infini.
Exemple
Soient A(z) = z 0
0 z
, B(z) = z 0
z z
et C(z) =
z 0 z−1 z
3 matrices L-unimodulaires, alors on a A(z)∼S B(z)∼S zI mais C(z)∼S
1 0 0 z2
(z = 0 ne fait pas perdre de rang de la même manière pour B(z) et C(z)) mais A(z)LS∼ B(z)LS∼ C(z)LS∼ I puisqu’elles sont L-unimodulaires !
On peut vérifier queU1(z)C(z)U2(z) =I avecU1(z) =
1 −1
−z−1+z−2 z−1 etU2(z) =
1 z 0 1
par exemple.
Remarquons que la somme des degrés des L-polynômes invariants deC(z) est égale à 0. En effet, la somme des degrés des L-polynômes invariants comp- tabilise tous les zéros sauf ceux qui sont en zéro ou l’infini. Le propre des matrices L-unimodulaires étant de n’avoir que des zéros en zéro ou l’infini, il est donc logique que cette somme vaille zéro pour C(z). Précisons enfin que pour l’application considérée (cf page 52) on déconvolue à une matrice de permutation et une matrice diagonale de retards près, les retards sont des zéros en l’infini, qui n’apparaissent donc pas dans les L-polynômes invariants, et n’influent donc pas sur la somme de ces degrés.